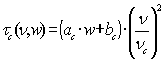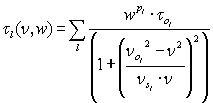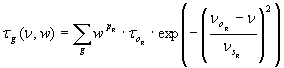| Bands at the 30m MRT, sizes of pixels and
arrays for various FOVs, Power load, NEP, NET, and NEFD from the background |
|
|
|
S.Leclercq - Nov 2009,
update Mar 2010 |
|
|
| The
numbered variables are the free parameters for the optical and photometric
calculations |
|
| The
grey font is used for comments or optional calculations given for information
but not used in the optical and photometric calculations |
|
|
| Diffraction
size on the 30m, number of beam and pixels per FOV |
|
|
FOV calculations not used
in the rest of the document: |
|
|
| Speed of light [m/s] c |
3E+08 |
|
|
input data |
|
|
| Boltzman constant [J/K] k |
1.38E-23 |
|
Planck RJ approx P[W]=2AWkTDn/l^2 |
HPBW angle ["] |
15 |
(Half Power Beam Width) |
|
|
| Planck constant [J*s] h |
6.63E-34 |
|
Flux F[10^26Jy]=P/(ADn)=2WkT/l^2 |
Pixel size [mm] |
2 |
(defines the optics of
the instrument, not the other way round !) |
|
|
|
|
Nb of pix per HPBW |
2 |
|
|
| M1 Diameter [m] |
30 |
|
FOV on detector |
40 |
mm |
FOV angle ['] |
7 |
|
| 1)
Wavelength [mm] |
3.25 |
2.05 |
1.25 |
0.87 |
|
|
result |
HPBW size [mm] |
4 |
|
|
| Frequency [GHz] n |
92 |
146 |
240 |
345 |
|
Nb of HPBW in FOV |
10.0 |
|
Nb of HPBW in FOV |
28.9 |
|
| Diffraction Pattern FWHM [mrad] |
112 |
70 |
43 |
30 |
|
FOV angle ['] |
2.4 |
|
FOV on detector |
115.7 |
mm |
|
| Diffraction Pattern FWHM ["] |
23 |
15 |
9 |
6 |
|
FOV on detector |
4.56 |
inches |
|
|
|
|
| Forward efficiency x (empiric fit) |
98% |
96% |
92% |
87% |
<= fit on the best
measures with ABCD receivers |
|
| Beam efficiency b (Ruze) |
78% |
72% |
58% |
39% |
Ruze (surface
deformations): b = 1.2*e0*exp(-((4s*Rs/l)^2)) |
|
| 2) Fraction
of unvigneted pupil diameter |
99% |
|
|
| Telescope effective area [m^2] A |
688 |
|
|
|
|
All the pixels in this
document are considered as bare (without horns), except for the MAMBO2 sheet |
|
| 3) Pixel
angular size u [Fl] |
1 |
|
|
0.5 |
|
| Pixel solid angle in the sky [sr] W |
1.2E-08 |
4.8E-09 |
1.8E-09 |
8.6E-10 |
|
3.0E-09 |
1.2E-09 |
4.5E-10 |
2.2E-10 |
|
| Throughput AW [mm^2sr] |
8.30 |
3.30 |
1.23 |
0.59 |
|
2.07 |
0.83 |
0.31 |
0.15 |
|
| AW/l^2 = (p/4)u^2 |
0.79 |
0.79 |
0.79 |
0.79 |
|
0.20 |
0.20 |
0.20 |
0.20 |
|
|
| Pixel efficiency on
diffraction spot z |
40% |
37% |
29% |
20% |
|
13% |
12% |
9% |
6% |
<= approximation from
gaussian fit on b |
|
|
3.14 |
3.14 |
3.14 |
3.14 |
|
Telescope focal |
F [m] |
292 |
|
| FOV diameter ['] |
Number pixels in FOV discs, rounded
at the upper group of 10s |
|
FOV diameter at the telescope focus
[cm] |
|
| 1 |
10 |
20 |
40 |
80 |
Total: |
30 |
60 |
150 |
300 |
Total: |
8.5 |
|
| 2 |
30 |
60 |
150 |
300 |
|
90 |
210 |
570 |
1170 |
|
17.0 |
|
| 3 |
50 |
120 |
320 |
660 |
|
190 |
480 |
1270 |
2620 |
|
25.5 |
|
| 4 |
90 |
210 |
570 |
1170 |
2040 |
340 |
840 |
2250 |
4650 |
8080 |
34.0 |
|
| 5 |
130 |
330 |
880 |
1820 |
|
520 |
1310 |
3520 |
7260 |
|
42.5 |
3/4 0.87 band |
|
| 6 |
190 |
480 |
1270 |
2620 |
|
750 |
1890 |
5060 |
10450 |
18150 |
51.0 |
3000 |
9950 |
|
| 7 |
260 |
640 |
1730 |
3560 |
6190 |
1020 |
2560 |
6890 |
14220 |
24690 |
59.5 |
4000 |
13450 |
|
| 8 |
340 |
840 |
2250 |
4650 |
|
1340 |
3350 |
9000 |
18570 |
|
68.0 |
|
| 9 |
430 |
1060 |
2850 |
5880 |
|
1690 |
4240 |
11390 |
23500 |
|
76.4 |
|
| 10 |
520 |
1310 |
3520 |
7260 |
12610 |
2080 |
5230 |
14060 |
29010 |
50380 |
84.9 |
|
| 11 |
630 |
1590 |
4260 |
8780 |
|
2520 |
6330 |
17010 |
35100 |
|
93.4 |
|
| 12 |
750 |
1890 |
5060 |
10450 |
|
3000 |
7530 |
20240 |
41780 |
|
101.9 |
|
|
| My simple ATM model |
|
| Based
on fits on ATM from Astro in Gildas, for the 50-400GHz range, with the error
constraint |Dt/t|<4% at 100kHz resolution in the
bands and 1MHz resolution in the atmospheric "walls", |
|
| built
with Tatm = 275 K, Psea_level = 1015 mb, Altitude = Pico Veleta (Tau~P and
Tau~T^3 => wv has the strongest effect in the range of possible P and T, |
|
| so my model
ignore dependence in T and P for simplicity) |
|
|
| Continuum |
|
| Reference frequency nc [GHz] |
250 |
|
|
225 |
|
| Water Vapor slope ac [1/mmwv] |
0.071 |
|
0.058 |
|
| Dry continnum at nc bc |
0.005 |
|
0.004 |
|
|
|
|
| Kinetic lines |
|
|
| Central frequency no [GHz] |
58.2 |
60.2 |
118.7 |
183.3 |
325.1 |
368.5 |
380.2 |
|
| Width ns [GHz] |
2.5 |
2 |
1 |
2.96 |
3.47 |
0.56 |
3.49 |
|
| Central tau to |
3.2 |
11.5 |
9.4 |
2.2 |
2 |
1 |
19 |
|
| Water power pl (0 = O2 line, 1 = H2O line) |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
|
|
|
| Gaussians
fitting groups of close-packeted lines |
|
|
|
| Central frequency no [GHz] |
58.1 |
62 |
65.3 |
440 |
|
| Width ns [GHz] |
2.5 |
2.1 |
3.1 |
80 |
|
| Central tau to |
17.6 |
20.2 |
0.2 |
0.13 |
|
| Water power pl (0 = O2 line, 1 = H2O line) |
0 |
0 |
0 |
1 |
|
|
| Simple photometry
calculations |
|
(reminder about unit
prefixes "a" = atto = 10^-18; m/a = 1/p) |
|
| Remarks
1: the RJ temperatures below are defined so that when used in the RJ
approximation formula of the brightness, the result = the unapproximated
Planck law |
|
| Remarks
2: the Power formula below assumes constant T (brightness) and h (overall efficiency) in the
integration over the bandwidth => correct @ <2 % error in the mm
atmospheric windows for T>2K |
| Remarks
3: the NET and NEFD are given for a choosen observing mode and for one pixel,
their value for a standard size (beam of HPBW) is given at the end of the
sheet |
|
|
| (Blockage M2 & quadurpod,
leackage) |
97% |
<= apparently not included in x since it has values > 98%... |
|
| 4) Cabin
optics transmission (M>2) |
95% |
<= transmission of M1
and M2 included in x, isn't it ? |
|
| 5) Cryostat
300K transmission |
95% |
88% |
<= total warm parts |
|
| 6) Cryostat
77K transmission |
86% |
|
|
|
| 7) Cryostat
4K transmission |
81% |
|
|
|
| 8) Band
pass filter transmission |
95% |
66% |
<= total cold parts |
|
| 9) Detector
absorbtion efficiency |
90% |
52% |
<= total optical chain |
|
| Global optical efficiency h |
51% |
50% |
48% |
45% |
<= total including
Feff |
|
|
|
Maximum bandwidth Dn_M defined by atmospheric
transmission >75% everywhere in the band for the water vapour chosen
below: |
| 10)
Bandwidht [GHz] Dn |
40 |
40 |
100 |
20 |
|
wv [mm] : |
7 |
5 |
4 |
2 |
1 |
|
| Band pass min freq [GHz] |
72 |
126 |
190 |
335 |
|
Dn_M : |
46 |
47 |
50 |
119 |
25 |
|
| Band pass max freq [GHz] |
112 |
166 |
290 |
355 |
|
Dn_M central n [GHz] : |
92 |
146.5 |
222 |
249.5 |
344.5 |
|
| Band pass min wave [mm] |
4.1 |
2.4 |
1.58 |
0.90 |
|
central l [mm] : |
3.26 |
2.05 |
1.35 |
1.20 |
0.87 |
|
| Band pass max wave [mm] |
2.7 |
1.8 |
1.03 |
0.85 |
|
| Bandwidth [mm] |
1.48 |
0.57 |
0.54 |
0.05 |
|
|
| 11) Degree
of polarization |
0 |
(0 = 2 polar = unpolarized, 1 = 1 polar) |
|
| Polarization parameter p |
1 |
|
| Quantic
effect of photons bunching on a surface ~ partial coherence factor (C) = covariance of the fluctuations
of intensity (= integral of integral of beam pattern for a point source) = 1
/ (available number of modes on the surface). |
|
| Asymptotes: (1) monomode or coherent or extended source: C = 1 ; (2) multimode
and incoherent point source: C ~= l^2/AW = 4/(pu^2) if u>3, C ~=
exp(-(0.6*u^((u+2)/(u+1))) if 0<u<3 (empricial approx by me). C can't
be >1. |
|
| 12) Spatial
coherance factor C |
1.0 |
0.5 |
1.3 |
|
1.0 |
0.8 |
5.1 |
(<= multimode pt
source approximations for u<3 and u>3 given for information) |
|
|
|
|
|
|
|
| 13)
Observing mode useful time ratio |
80% |
(e.g. 80% for OTF, 45% for On-Off) |
|
| Observing mode efficiency g |
1.12 |
<= includes the
"reference+source" *2^0.5 factor and "frequency to time"
/2^0.5 factors which cancel each other |
|
|
|
|
| NEP
to NET = T/P(T) = Q/exp(-t) ;
NEP to NEFD = F/P(F) = J/exp(-t) (Q and J are defined such that they don't depend on the
atmospheric conditions) |
|
| Q = pl^2/(2kAWhDn) [K/pW] |
2.3 |
2.3 |
1.0 |
5.1 |
|
9.0 |
9.2 |
3.8 |
20.3 |
|
| J = px/(AhzDn) [Jy/pW] |
17 |
19 |
10 |
70 |
|
55 |
60 |
30 |
220 |
|
| T/F: (Q/J)(x/z) = (l^2/2kW) =
D^2/2ku^2 [K/Jy] |
0.32 |
0.32 |
0.32 |
|
|
1.27 |
1.27 |
1.27 |
|
|
|
| x/z |
2.46 |
2.61 |
3.15 |
4.38 |
|
7.72 |
8.21 |
9.89 |
13.76 |
|
|
| Atmosphere |
|
|
| 14)
Atmosphere temperature (Ta) [K] |
275 |
|
| Black body occupation number
at n |
62 |
39 |
23 |
16 |
|
| Brightness for frequencies
[fW/m^2/Hz/sr] |
0.7 |
1.8 |
4.8 |
9.7 |
|
| (RJ approx brightness
[fW/m^2/Hz/sr]) |
0.7 |
1.8 |
4.9 |
10.0 |
|
| Black body RJ temperature T
[K] |
273 |
272 |
269 |
267 |
|
|
|
|
| 15)
Elevation [deg] |
60 |
|
|
|
| Airmass |
1.15 |
|
|
|
|
|
|
| 16)
Precipitable water vapor (wv) [mm] |
1 |
|
| Opacity tau meter (225GHz) |
0.06 |
<= from IRAM Spain weather page
(http://www.iram.es/IRAMES/weather.html), after Nov 16 correction; old was
for Atacama ==> |
0.05 |
|
| Opacity tau meter (225GHz) |
0.06 |
<= from the continuum part only (lines
negligible at 225Ghz) of my simplified ATM model |
|
|
Opacity components for each band: |
|
| Atm continuum only |
0.010 |
0.026 |
0.070 |
0.145 |
|
| Atm O2 kinetic lines |
0.025 |
0.008 |
0.002 |
0.001 |
|
| Atm H2O kinetic lines |
0.000 |
0.003 |
0.004 |
0.058 |
|
| Atm O2 gaussian bunch |
0.000 |
0.000 |
0.000 |
0.000 |
|
| Atm H2O gaussian bunch |
0.000 |
0.000 |
0.000 |
0.000 |
|
| Atm total t (including airmass) |
0.04 |
0.04 |
0.09 |
0.235 |
|
| Emissivity |
4% |
4% |
8% |
21% |
|
|
| Spectral radiance of
atmosphere [fW/m^2/Hz/sr] |
0.03 |
0.08 |
0.40 |
2.04 |
|
| Atmos emission T RJ [K] T |
11 |
11 |
23 |
56 |
|
|
|
|
| Power [pW] P=(2AWh/p)kTDn/l^2 |
4.9 |
5.0 |
23.5 |
11.0 |
|
1.2 |
1.2 |
5.9 |
2.8 |
|
|
|
|
|
|
| NEPp = (2hnP)^0.5 [aW/Hz^0.5] |
25 |
31 |
87 |
71 |
|
12 |
16 |
43 |
35 |
|
| NEPb = P(pC/Dn)^0.5 [aW/Hz^0.5] |
25 |
25 |
74 |
78 |
|
6 |
6 |
19 |
19 |
|
| NEP |
35 |
40 |
114 |
105 |
|
14 |
17 |
47 |
40 |
|
|
| NETp = gNEPpQ/exp(-t)
[mK*s^0.5] |
0.06 |
0.08 |
0.10 |
0.51 |
|
0.13 |
0.17 |
0.20 |
1.02 |
|
| NETb = gNEPbQ/exp(-t)
[mK*s^0.5] |
0.06 |
0.07 |
0.09 |
0.56 |
|
0.06 |
0.07 |
0.09 |
0.56 |
|
| NET |
0.09 |
0.11 |
0.13 |
0.76 |
|
0.14 |
0.18 |
0.22 |
1.16 |
|
|
| NEFDp = gNEPpJ/exp(-t)
[mJy*s^0.5] |
0.5 |
0.7 |
1.0 |
7.0 |
|
0.8 |
1.1 |
1.6 |
11.4 |
|
| NEFDb = gNEPbJ/exp(-t)
[mJy*s^0.5] |
0.5 |
0.6 |
0.9 |
7.7 |
|
0.4 |
0.4 |
0.7 |
6.3 |
|
| NEFD |
0.7 |
0.9 |
1.3 |
10.4 |
|
0.9 |
1.2 |
1.7 |
13.0 |
|
|
|
|
| Spillover |
|
|
| Temperature of environment
behind M1 [K] |
275 |
|
| Emissivity |
2% |
4% |
8% |
13% |
|
| Spectral radiance of behind
M1 [fW/m^2/Hz/sr] |
0.02 |
0.07 |
0.38 |
1.27 |
|
| T RJ [K] |
5.7 |
10.9 |
21.5 |
34.9 |
|
|
|
|
| Power [pW] P=(2AWh/p)kTDn/l^2 |
2.6 |
4.9 |
24.4 |
7.9 |
|
0.6 |
1.2 |
6.1 |
2.0 |
|
|
|
| NEPp = (2hnP)^0.5 [aW/Hz^0.5] |
18 |
31 |
88 |
60 |
|
9 |
15 |
44 |
30 |
|
| NEPb = P(pC/Dn)^0.5 [aW/Hz^0.5] |
13 |
25 |
77 |
56 |
|
3 |
6 |
19 |
14 |
|
| NEP |
22 |
40 |
117 |
82 |
|
9 |
17 |
48 |
33 |
|
|
| NETp = gNEPpQ/exp(-t)
[mK*s^0.5] |
0.05 |
0.08 |
0.10 |
0.43 |
|
0.09 |
0.17 |
0.21 |
0.86 |
|
| NETb = gNEPbQ/exp(-t)
[mK*s^0.5] |
0.03 |
0.07 |
0.09 |
0.40 |
|
0.03 |
0.07 |
0.09 |
0.40 |
|
| NET |
0.06 |
0.11 |
0.14 |
0.59 |
|
0.10 |
0.18 |
0.23 |
0.95 |
|
|
| NEFDp = gNEPpJ/exp(-t)
[mJy*s^0.5] |
0.4 |
0.7 |
1.0 |
6.0 |
|
0.6 |
1.1 |
1.6 |
9.4 |
|
| NEFDb = gNEPbJ/exp(-t)
[mJy*s^0.5] |
0.3 |
0.5 |
0.9 |
5.5 |
|
0.2 |
0.4 |
0.7 |
4.3 |
|
| NEFD |
0.4 |
0.9 |
1.4 |
8.1 |
|
0.6 |
1.2 |
1.8 |
10.3 |
|
|
|
|
| 300K optics |
|
|
| (17) Mean
surface temperature [K] |
280 |
|
| Black body occupation number
at n |
63 |
39 |
24 |
16 |
|
| Black body RJ temperature T
[K] |
278 |
277 |
274 |
272 |
|
| Emissivity mirrors / cryostat |
4.9% |
5.0% |
|
| Spectral radiance of mirrors
[fW/m^2/Hz/sr] |
0.04 |
0.09 |
0.24 |
0.49 |
|
| Spectral radiance of warm
optics [fW/m^2/Hz/sr] |
0.04 |
0.09 |
0.24 |
0.50 |
|
| T RJ for mirrors [K] |
13.6 |
13.6 |
13.4 |
13.3 |
|
| T RJ for cryostat warm optics [K] |
13.9 |
13.8 |
13.7 |
13.6 |
|
| For P: apply x to mirrors (correct or not ?) but not to cryostat 300K |
|
| Power [pW] P=(2AWh/p)kTDn/l^2 |
13.7 |
13.6 |
33.3 |
6.5 |
|
3.4 |
3.4 |
8.3 |
1.6 |
|
|
| NEPp = (2hnP)^0.5 [aW/Hz^0.5] |
41 |
51 |
103 |
54 |
|
20 |
26 |
51 |
27 |
|
| NEPb = P(pC/Dn)^0.5 [aW/Hz^0.5] |
69 |
68 |
105 |
46 |
|
17 |
17 |
26 |
11 |
|
| NEP |
80 |
85 |
147 |
71 |
|
27 |
31 |
58 |
30 |
|
|
| NETp = gNEPpQ/exp(-t)
[mK*s^0.5] |
0.11 |
0.14 |
0.12 |
0.39 |
|
0.22 |
0.28 |
0.24 |
0.78 |
|
| NETb = gNEPbQ/exp(-t)
[mK*s^0.5] |
0.18 |
0.18 |
0.12 |
0.33 |
|
0.18 |
0.18 |
0.12 |
0.33 |
|
| NET |
0.21 |
0.23 |
0.17 |
0.51 |
|
0.28 |
0.33 |
0.27 |
0.85 |
|
|
| NEFDp = gNEPpJ/exp(-t)
[mJy*s^0.5] |
0.8 |
1.1 |
1.2 |
5.4 |
|
1.3 |
1.8 |
1.9 |
8.5 |
|
| NEFDb = gNEPbJ/exp(-t)
[mJy*s^0.5] |
1.4 |
1.5 |
1.2 |
4.6 |
|
1.1 |
1.2 |
1.0 |
3.6 |
|
| NEFD |
1.6 |
1.9 |
1.7 |
7.1 |
|
1.7 |
2.1 |
2.1 |
9.2 |
|
|
|
|
| 77K stage |
|
|
| Temperature cryostat optics
on N2 stage [K] |
77 |
|
| Black body occupation number
at n |
17 |
10 |
6 |
4 |
|
| Black body RJ temperature T
[K] |
75 |
74 |
71 |
69 |
|
| Emissivity |
14% |
|
| Spectral radiance of N2 stage
[fW/m^2/Hz/sr] |
0.03 |
0.07 |
0.18 |
0.36 |
|
| T RJ for [K] |
10.7 |
10.5 |
10.2 |
9.8 |
|
|
| Power [pW] P=(2AWh/p)kTDn/l^2 |
6.4 |
6.3 |
15.3 |
3.0 |
|
1.6 |
1.6 |
3.8 |
0.7 |
|
|
| NEPp = (2hnP)^0.5 [aW/Hz^0.5] |
28 |
35 |
70 |
37 |
|
14 |
18 |
35 |
18 |
|
| NEPb = P(pC/Dn)^0.5 [aW/Hz^0.5] |
32 |
32 |
48 |
21 |
|
8 |
8 |
12 |
5 |
|
| NEP |
43 |
47 |
85 |
42 |
|
16 |
19 |
37 |
19 |
|
|
| NETp = gNEPpQ/exp(-t)
[mK*s^0.5] |
0.07 |
0.09 |
0.08 |
0.26 |
|
0.15 |
0.19 |
0.16 |
0.53 |
|
| NETb = gNEPbQ/exp(-t)
[mK*s^0.5] |
0.08 |
0.08 |
0.06 |
0.15 |
|
0.08 |
0.08 |
0.06 |
0.15 |
|
| NET |
0.11 |
0.13 |
0.10 |
0.30 |
|
0.17 |
0.21 |
0.17 |
0.55 |
|
|
| NEFDp = gNEPpJ/exp(-t)
[mJy*s^0.5] |
0.6 |
0.8 |
0.8 |
3.7 |
|
0.9 |
1.2 |
1.3 |
5.7 |
|
| NEFDb = gNEPbJ/exp(-t)
[mJy*s^0.5] |
0.7 |
0.7 |
0.6 |
2.1 |
|
0.5 |
0.5 |
0.4 |
1.6 |
|
| NEFD |
0.9 |
1.0 |
1.0 |
4.2 |
|
1.0 |
1.3 |
1.3 |
6.0 |
|
|
| TOTAL BACKGROUD |
|
|
|
| Power [pW] |
28 |
30 |
97 |
28 |
|
7 |
7 |
24 |
7 |
|
|
| NEPp = (2hnP)^0.5 [aW/Hz^0.5] |
58 |
76 |
175 |
114 |
|
29 |
38 |
88 |
57 |
|
| NEPb = P(pC/Dn)^0.5 [aW/Hz^0.5] |
138 |
149 |
305 |
200 |
|
35 |
37 |
76 |
50 |
|
| NEP [aW/Hz^0.5] |
150 |
167 |
352 |
231 |
|
45 |
53 |
116 |
76 |
|
|
| NETp = gNEPpQ/exp(-t)
[mK*s^0.5] |
0.15 |
0.20 |
0.21 |
0.82 |
|
0.31 |
0.41 |
0.41 |
1.64 |
|
| NETb = gNEPbQ/exp(-t)
[mK*s^0.5] |
0.36 |
0.40 |
0.36 |
1.44 |
|
0.36 |
0.40 |
0.36 |
1.44 |
|
| NET [mK*s^0.5] |
0.39 |
0.45 |
0.41 |
1.66 |
|
0.48 |
0.57 |
0.54 |
2.18 |
|
|
|
|
1.20 |
1.27 |
1.32 |
1.32 |
|
| NEFDp = gNEPpJ/exp(-t)
[mJy*s^0.5] |
1.2 |
1.7 |
2.0 |
11.3 |
|
1.9 |
2.6 |
3.2 |
17.7 |
|
| NEFDb = gNEPbJ/exp(-t)
[mJy*s^0.5] |
2.8 |
3.3 |
3.5 |
19.9 |
|
2.2 |
2.6 |
2.8 |
15.6 |
|
| NEFD [mJy*s^0.5] |
3.1 |
3.7 |
4.1 |
22.9 |
|
2.9 |
3.7 |
4.2 |
23.6 |
|
|
0.95 |
1.00 |
1.04 |
1.03 |
|
| TOTAL
BACKGROUD for a standard elementary size |
|
|
| (18)
Standard elementary size us
[Fl] |
1.1 |
Comon standard sizes:
"beam" = 2*1.22 = 1st dark ring of the Airy diffraction pattern ~=
2 ; "HPBW" = "FWHM" = 1.03 ~= 1 |
|
| (19)
spatial coherence factor Cs |
1 |
(<= extended source) |
0.5 |
1.1 |
(<= incoherent point
source case given for information, note that NEPb becomes poissonian like
NEPp only when C = l^2/AW !) |
| Diffractive gaussian
efficiency zs |
45% |
42% |
33% |
23% |
|
|
|
| zs/z |
1.1 |
1.1 |
1.1 |
1.1 |
|
3.6 |
3.6 |
3.6 |
3.6 |
|
|
|
| T/F [K/Jy] |
0.26 |
|
F/T |
3.81 |
|
| P ~
(us/u)^2 [pW] |
33 |
36 |
117 |
34 |
|
33 |
36 |
117 |
34 |
|
|
!! In case of incoherent
signal C~1/u^2 => the NEXb behave like the NEXp ; they become Poissonian
!! |
|
|
| NEPp ~ (us/u) |
64 |
84 |
193 |
125 |
|
64 |
84 |
193 |
125 |
|
| NEPb ~ (us/u)^2*(Cs/C)^0.5 |
167 |
181 |
369 |
243 |
|
167 |
181 |
369 |
243 |
|
| NEP [aW/Hz^0.5] |
179 |
199 |
417 |
273 |
|
179 |
199 |
417 |
273 |
|
|
|
|
| NETp ~ 1/(us/u) |
0.14 |
0.19 |
0.19 |
0.74 |
|
0.14 |
0.19 |
0.19 |
0.74 |
|
| NETb ~ (Cs/C)^0.5 |
0.36 |
0.40 |
0.36 |
1.44 |
|
0.36 |
0.40 |
0.36 |
1.44 |
|
| NET [mK*s^0.5] |
0.39 |
0.44 |
0.40 |
1.62 |
|
0.39 |
0.44 |
0.40 |
1.62 |
|
|
|
|
|
|
| NEFDp ~ (us/u)/(zs/z) |
1.1 |
1.6 |
2.0 |
10.9 |
|
1.1 |
1.6 |
2.0 |
10.9 |
|
| NEFDb ~ (us/u)^2*(Cs/C)^0.5/(zs/z) |
3.0 |
3.5 |
3.8 |
21.2 |
|
3.0 |
3.5 |
3.8 |
21.2 |
|
| NEFD [mJy*s^0.5] |
3.2 |
3.9 |
4.3 |
23.8 |
|
3.2 |
3.9 |
4.3 |
23.8 |
|
|
| Power from a source in a
pixel |
|
|
| T RJ of the source seen by the pixel [K] |
50 |
|
|
| Power [pW] P=(2AWe-th/p)kTDn/l^2 |
21 |
21 |
48 |
8 |
|
5 |
5 |
13 |
2 |
|
| total TRJ + Tbkg [pW] |
49 |
51 |
144 |
36 |
|
12 |
13 |
37 |
9 |
|
|
|
|
| Flux of the source [Jy] |
500 |
|
| Power [pW] P=(FAe-thz/xp)Dn |
27 |
25 |
48 |
6 |
|
9 |
8 |
15 |
2 |
|
|
| Dynamic: Pmax/Pmin |
2.8 |
3.4 |
3.4 |
2.6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|