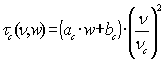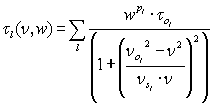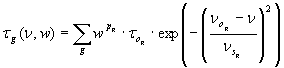| Bands at the 30m MRT, sizes of pixels and
arrays for various FOVs, Power load, NEP, NET, and NEFD from the background |
|
|
|
S.Leclercq - Nov 2009 |
|
|
| The
numbered variables are the free parameters for the optical and photometric
calculations |
|
| The
grey font is used for comments or optional calculations given for information
but not used in the optical and photometric calculations |
|
|
| Diffraction
size on the 30m, number of beam and pixels per FOV |
|
|
| Speed of light [m/s] c |
3E+08 |
|
| Boltzman constant [J/K] k |
1.38E-23 |
|
| Planck constant [J*s] h |
6.63E-34 |
|
|
|
|
| M1 Diameter [m] |
30 |
|
| 1)
Wavelength [mm] l |
1.2 |
|
| Frequency [GHz] n |
250 |
|
| Diffraction Pattern FWHM [mrad] |
41 |
|
| Diffraction Pattern FWHM (HPBW) ["] |
8 |
|
|
|
|
| Forward efficiency x (empiric fit) |
92% |
|
|
| Beam efficiency b (Ruze) |
56% |
|
| 2)
Fraction of unvigneted pupil diameter |
100% |
<= No cold pupil,
but the pixel creates its own vigneting through the horn taper function (see W) |
|
| Telescope effective area
[m^2] A |
707 |
=> area defining the diffraction at horn
input: not useful, the relevant effective area is defined by the horn taper
illumination, see below |
|
|
|
|
| 3) Pixel
angular size u [Fl] |
2 |
<= based on the
measured HPBW would be 1.3, but incompatible with Griffin !!! must find the
problem !!! |
|
| Pixel solid angle in the sky [sr] W |
1.8E-09 |
<= defined with the horn
spill-over (hs, see below) and A (not significant quantity, the important quantity for the calculations is AW) |
|
| Throughput AW [mm^2sr] |
1.25 |
<= defined with hs/l^2, so depends only on hs, which is the
integral of taper function up to the edge of the antena |
|
|
| Horn spill-over: hs = AW/l^2 |
0.86 |
<= assumes a edge taper Te =
2.2*u^2, I didn't
find a reference allowing to find the actual hs, but
it is compatible with geometries described in Goldsmith |
| Pixel efficiency on
diffraction spot z |
53% |
|
|
| FOV diameter ['] |
Number pixels in FOV discs, rounded
at the upper group of 10s |
|
| 1 |
10 |
|
| 2 |
40 |
|
| 3 |
90 |
|
|
|
| 4 |
160 |
|
| 5 |
250 |
|
|
| 6 |
360 |
|
| 7 |
480 |
|
| 8 |
630 |
|
| 9 |
800 |
|
| 10 |
980 |
|
|
| 11 |
1190 |
|
| 12 |
1410 |
|
|
| My simple ATM model |
|
| Based
on fits on ATM from Astro in Gildas, for the 50-400GHz range, with the error
constraint |Dt/t|<4% at 100kHz resolution in the
bands and 1MHz resolution in the atmospheric "walls", |
|
| built
with Tatm = 275 K, Psea_level = 1015 mb, Altitude = Pico Veleta (Tau~P and
Tau~T^3 => wv has the strongest effect in the range of possible P and T, |
|
| so my model
ignore dependence in T and P for simplicity) |
|
|
| Continuum |
|
| Reference frequency nc [GHz] |
250 |
|
|
225 |
|
| Water Vapor slope ac [1/mmwv] |
0.071 |
|
0.058 |
|
| Dry continnum at nc bc |
0.005 |
|
0.004 |
|
|
|
|
| Kinetic lines |
|
|
| Central frequency no [GHz] |
58.2 |
60.2 |
118.7 |
183.3 |
325.1 |
368.5 |
380.2 |
|
| Width ns [GHz] |
2.5 |
2 |
1 |
2.96 |
3.47 |
0.56 |
3.49 |
|
| Central tau to |
3.2 |
11.5 |
9.4 |
2.2 |
2 |
1 |
19 |
|
| Water power pl (0 = O2 line, 1 = H2O line) |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
|
|
|
| Gaussians
fitting groups of close-packeted lines |
|
|
|
| Central frequency no [GHz] |
58.1 |
62 |
65.3 |
440 |
|
| Width ns [GHz] |
2.5 |
2.1 |
3.1 |
80 |
|
| Central tau to |
17.6 |
20.2 |
0.2 |
0.13 |
|
| Water power pl (0 = O2 line, 1 = H2O line) |
0 |
0 |
0 |
1 |
|
|
| Simple photometry
calculations |
|
(reminder for the units of NEP:
prefix "a" = atto = 10^-18) |
|
| Remarks
1: the RJ temperatures below are defined so that when used in the RJ
approximation formula of the brightness, the result = the unapproximated
Planck law |
|
| Remarks
2: the Power formula below assumes constant T (brightness) and h (overall efficiency) in the
integration over the bandwidth => correct @ <2 % error in the mm
atmospheric windows for T>2K |
| Remarks
3: the NET and NEFD are given for a choosen observing mode and for one pixel,
their value for a standard size (beam of HPBW) is given at the end of the
sheet |
|
|
| (Blockage M2 & quadurpod,
leackage) |
97% |
|
| 4) Cabin
optics transmission (M>2) |
94% |
|
| 5) Cryostat
300K transmission |
90% |
85% |
<= total warm parts |
|
| 6) Cryostat
77K transmission |
86% |
|
|
|
| 7) Cryostat
4K transmission |
86% |
|
|
| 8) Band
pass filter transmission |
95% |
70% |
<= total cold parts |
|
| 9) Detector
absorbtion efficiency |
80% |
47% |
<= total optical chain |
|
| Global optical efficiency h |
42% |
|
|
|
|
|
|
|
| 10)
Bandwidht [GHz] Dn |
100 |
|
| Band pass min freq [GHz] |
200 |
|
| Band pass max freq [GHz] |
300 |
|
| Band pass min wave [mm] |
1.5 |
|
| Band pass max wave [mm] |
1.0 |
|
| Bandwidth [mm] |
0.50 |
|
|
| 11) Degree
of polarization |
0 |
|
| Polarization parameter p |
1 |
|
|
|
| monomode or coherent or extended source: C = 1 ; multimode and
incoherent point source: C ~= l^2/AW = 4/(pu^2) if u>3, C ~=
exp(-(0.6*u^((u+2)/(u+1))) if 0<u<3 (empricial approx by me). C can't
be >1. |
|
| 12) Spatial
coherance factor C |
1.0 |
0.2 |
0.3 |
|
|
|
|
| 13)
Observing mode useful time ratio |
45% |
<= OnOff |
|
| Observing mode efficiency g |
1.49 |
|
|
|
|
| NEP
to NET = T/P(T) = Q/exp(-t) ;
NEP to NEFD = F/P(F) = J/exp(-t) (Q and J are defined such that they don't depend on the
atmospheric conditions) |
|
| Q = pl^2/(2kAWhDn) [K/pW] |
1.0 |
|
| J = px/(AhzDn) [Jy/pW] |
6 |
|
| T/F: (Q/J)(x/z) = (l^2/2kW) =
D^2/2ku^2 [K/Jy] |
0.30 |
0.30 |
0.08 |
|
| x/z |
1.72 |
|
| Atmosphere |
|
|
| 14)
Atmosphere temperature (Ta) [K] |
275 |
|
| Black body occupation number
at n |
22 |
|
| Brightness for frequencies
[fW/m^2/Hz/sr] |
5.2 |
|
| (RJ approx brightness
[fW/m^2/Hz/sr]) |
5.3 |
|
| Black body RJ temperature T
[K] |
269 |
|
|
|
|
| 15)
Elevation [deg] |
60 |
|
| Airmass |
1.15 |
|
|
|
|
| 16)
Precipitable water vapor (wv) [mm] |
1 |
|
| Opacity tau meter (225GHz) |
0.06 |
|
| Opacity tau meter (225GHz) |
0.06 |
|
|
Opacity components for each band: |
|
| Atm continuum only |
0.076 |
|
| Atm O2 kinetic lines |
0.001 |
|
| Atm H2O kinetic lines |
0.004 |
|
| Atm O2 gaussian bunch |
0.000 |
|
| Atm H2O gaussian bunch |
0.000 |
|
| Atm total t (including airmass) |
0.10 |
|
| Emissivity |
9% |
|
|
| Spectral radiance of
atmosphere [fW/m^2/Hz/sr] |
0.47 |
|
| Atmos emission T RJ [K] T |
24 |
|
|
| Power [pW] P=(2AWh/p)kTDn/l^2 |
24.6 |
|
|
|
|
| NEPp = (2hnP)^0.5 [aW/Hz^0.5] |
90 |
|
| NEPb = P(pC/Dn)^0.5 [aW/Hz^0.5] |
78 |
|
| NEP |
119 |
|
|
| NETp = gNEPpQ/exp(-t)
[mK*s^0.5] |
0.15 |
|
| NETb = gNEPbQ/exp(-t)
[mK*s^0.5] |
0.13 |
|
| NET |
0.19 |
|
|
| NEFDp = gNEPpJ/exp(-t)
[mJy*s^0.5] |
0.9 |
|
| NEFDb = gNEPbJ/exp(-t)
[mJy*s^0.5] |
0.7 |
|
| NEFD |
1.1 |
|
|
|
|
| Spillover |
|
|
| Temperature of environment
behind M1 [K] |
275 |
|
| Emissivity |
8% |
|
| Spectral radiance of behind
M1 [fW/m^2/Hz/sr] |
0.44 |
|
| T RJ [K] |
22.8 |
|
|
|
|
| Power [pW] P=(2AWh/p)kTDn/l^2 |
25.0 |
3.9% |
|
|
|
| NEPp = (2hnP)^0.5 [aW/Hz^0.5] |
91 |
|
| NEPb = P(pC/Dn)^0.5 [aW/Hz^0.5] |
79 |
|
| NEP |
121 |
|
|
| NETp = gNEPpQ/exp(-t)
[mK*s^0.5] |
0.15 |
|
| NETb = gNEPbQ/exp(-t)
[mK*s^0.5] |
0.13 |
|
| NET |
0.20 |
|
|
| NEFDp = gNEPpJ/exp(-t)
[mJy*s^0.5] |
0.9 |
|
| NEFDb = gNEPbJ/exp(-t)
[mJy*s^0.5] |
0.7 |
|
| NEFD |
1.1 |
|
|
|
|
| 300K optics |
|
|
| (17) Mean
surface temperature [K] |
280 |
|
| Black body occupation number
at n |
23 |
|
| Black body RJ temperature T
[K] |
274 |
|
| Emissivity mirrors / cryostat |
5.9% |
9.8% |
15% |
<= emissivity of
system mirrors + cryostat |
|
| Spectral radiance of mirrors
[fW/m^2/Hz/sr] |
0.31 |
|
|
|
| Spectral radiance of warm
optics [fW/m^2/Hz/sr] |
0.51 |
|
|
|
| T RJ for mirrors [K] |
16.0 |
|
41.2 |
<= system mirrors +
cryostat |
|
| T RJ for cryostat warm optics [K] |
26.7 |
|
|
|
| For P: apply x to mirrors (correct or not ?) but not to cryostat 300K |
|
| Power [pW] P=(2AWh/p)kTDn/l^2 |
53.3 |
|
54.9 |
50.3 |
<= system mirrors +
cryostat with/without x |
|
| details of P: mirror /
cryostat |
17.7 |
35.6 |
|
| NEPp = (2hnP)^0.5 [aW/Hz^0.5] |
133 |
|
| NEPb = P(pC/Dn)^0.5 [aW/Hz^0.5] |
169 |
|
| NEP |
215 |
|
|
| NETp = gNEPpQ/exp(-t)
[mK*s^0.5] |
0.22 |
|
| NETb = gNEPbQ/exp(-t)
[mK*s^0.5] |
0.27 |
|
| NET |
0.35 |
|
|
| NEFDp = gNEPpJ/exp(-t)
[mJy*s^0.5] |
1.3 |
|
| NEFDb = gNEPbJ/exp(-t)
[mJy*s^0.5] |
1.6 |
|
| NEFD |
2.0 |
|
|
|
|
| 77K stage |
|
|
| Temperature cryostat optics
on N2 stage [K] |
77 |
|
| Black body occupation number
at n |
6 |
|
| Black body RJ temperature T
[K] |
71 |
|
| Emissivity |
14% |
|
| Spectral radiance of N2 stage
[fW/m^2/Hz/sr] |
0.19 |
|
| T RJ for [K] |
10 |
|
|
| Power [pW] P=(2AWh/p)kTDn/l^2 |
15.8 |
|
|
|
| NEPp = (2hnP)^0.5 [aW/Hz^0.5] |
72 |
|
| NEPb = P(pC/Dn)^0.5 [aW/Hz^0.5] |
50 |
|
| NEP |
88 |
|
|
| NETp = gNEPpQ/exp(-t)
[mK*s^0.5] |
0.12 |
|
| NETb = gNEPbQ/exp(-t)
[mK*s^0.5] |
0.08 |
|
| NET |
0.14 |
|
|
| NEFDp = gNEPpJ/exp(-t)
[mJy*s^0.5] |
0.7 |
|
| NEFDb = gNEPbJ/exp(-t)
[mJy*s^0.5] |
0.5 |
|
| NEFD |
0.8 |
|
|
| TOTAL BACKGROUD |
|
|
|
| Power [pW] |
119 |
|
mapping estimator (my try, need to
check iram web page time estimator, and values in CT proposal): |
|
|
aa = angular coverage in sky of 117
pix [as^2] |
11119 |
|
| NEPp = (2hnP)^0.5 [aW/Hz^0.5] |
198 |
|
am = angular size of the map [as^2]
(must be > aa (*)) |
90000 |
|
| NEPb = P(pC/Dn)^0.5 [aW/Hz^0.5] |
375 |
|
ff = filling factor (only for am
> aa (*)) |
|
8 |
|
| NEP [aW/Hz^0.5] |
424 |
|
ti = integration time [h] |
|
|
8 |
|
|
rms assuming homogeneous ti on the
map [mJy] |
0.19 |
|
| NETp = gNEPpQ/exp(-t)
[mK*s^0.5] |
0.32 |
|
verification of the method: |
|
| NETb = gNEPbQ/exp(-t)
[mK*s^0.5] |
0.61 |
|
NEFD from CT proposal [mJy*s^0.5] |
|
45 |
|
| NET [mK*s^0.5] |
0.69 |
|
rms assuming homogeneous ti on the
map [mJy] |
2.15 |
|
|
|
|
| NEFDp = gNEPpJ/exp(-t)
[mJy*s^0.5] |
1.9 |
|
(*) if am < aa, need to
calculate the nb of pixelsto use & subscan necessary to fill the gaps
between pixel |
|
| NEFDb = gNEPbJ/exp(-t)
[mJy*s^0.5] |
3.6 |
|
|
|
| NEFD [mJy*s^0.5] |
4.0 |
|
|
|
|
| TOTAL
BACKGROUD for a standard elementary size |
|
|
| (18)
Standard elementary size us
[Fl] |
2.44 |
|
| (19)
spatial coherence factor Cs |
1 |
(<= extended source) |
0.1 |
0.2 |
(<= incoherent point
source approxs : u<3 and u>3) |
|
| Diffractive gaussian
efficiency zs |
56% |
|
| zs/z |
1.05 |
|
|
| P ~
(us/u)^2 [pW] |
176.6 |
|
|
| NEPp ~ (us/u) |
242 |
|
| NEPb ~ (us/u)^2*(Cs/C)^0.5 |
559 |
|
| NEP [aW/Hz^0.5] |
609 |
|
|
| NETp ~ 1/(us/u) |
0.26 |
|
| NETb ~ (Cs/C)^0.5 |
0.61 |
|
| NET [mK*s^0.5] |
0.67 |
|
|
|
|
| NEFDp ~ (us/u)/(zs/z) |
2.2 |
|
| NEFDb ~ (us/u)^2*(Cs/C)^0.5/(zs/z) |
5.0 |
|
| NEFD [mJy*s^0.5] |
5.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|